Fichiers-txt
Les fonctions
DEFINITION
Note
La programmation est l’art d’apprendre à un ordinateur comment accomplir des tâches qu’il n’était pas capable de réaliser
auparavant. L’une des méthodes les plus intéressantes pour y arriver consiste à ajouter de nouvelles instructions au langage de programmation que vous utilisez, sous la forme de fonctions originales.
Définir une fonction
Note
Les scripts que vous avez écrits jusqu’à présent étaient à chaque fois très courts, car leur objectif était seulement de vous faire assimiler les premiers éléments du langage.
Lorsque vous commencerez à développer de véritables projets, vous serez confrontés à des problèmes souvent forts complexes, et les lignes de programme vont commencer à s’accumuler…
L’approche efficace d’un problème complexe consiste souvent à le décomposer en plusieurs sous-problèmes plus simples qui seront étudiés séparément (ces sous-problèmes peuvent éventuellement être eux-mêmes décomposés à leur tour, et ainsi de suite).
D’autre part, il arrivera souvent qu’une même séquence d’instructions doive être utilisée à plusieurs reprises dans un programme.
FONCTIONS ET PROCEDURES
La syntaxe Python pour la définition d’une fonction est la suivante :
def nom_de_la_fonction(paramètres) :
{indentation} Bloc d’instructions
Vous pouvez choisir n’importe quel nom pour la fonction que vous créez, à l’exception des mots réservés du langage, et à la condition de n’utiliser aucun caractère spécial ou accentué (le caractère souligné » _ » est permis). Comme c’est le cas pour les noms de variables, il vous est conseillé d’utiliser surtout des lettres minuscules, notamment au début du nom (les noms commençant par une majuscule seront réservés aux classes. Comme les instructions if et while que vous connaissez déjà, l’instruction def est une instruction composée. La ligne contenant cette instruction se termine obligatoirement par un double point, lequel introduit un bloc d’instructions que vous ne devez pas oublier d’indenter. La liste de paramètres spécifie quelles informations il faudra fournir en guise d’arguments lorsque l’on voudra utiliser cette fonction (les parenthèses peuvent parfaitement rester vides si la fonction ne nécessite pas d’arguments). Une fonction s’utilise pratiquement comme une instruction quelconque. Dans le corps d’un programme, un appel de fonction est constitué du nom de la fonction suivi de parenthèses. Si c’est nécessaire, on place dans ces parenthèses le ou les arguments que l’on souhaite transmettre à la fonction. Il faudra en principe fournir un argument pour chacun des paramètres spécifiés dans la définition de la fonction, encore qu’il soit possible de définir pour ces paramètres des valeurs par défaut.
Exemple 0501 :
Programme
Résultat
#fonction_multiplication.py
# définir une fonction
def table(base):
n=1
while n<10:
print(n,'x',base,'= ',n*base, ' ;')
n=n+1
#programme principal
base=int(input("Entrer un nombre entier :"))
table(base) # appel de la fonction
Entrer un nombre entier :5
1 x 5 = 5 ;
2 x 5 = 10 ;
3 x 5 = 15 ;
4 x 5 = 20 ;
5 x 5 = 25 ;
6 x 5 = 30 ;
7 x 5 = 35 ;
8 x 5 = 40 ;
9 x 5 = 45 ;
VRAIES FONCTIONS
Pour les puristes, les fonctions que nous avons décrites jusqu’à présent ne sont pas tout à fait des fonctions au sens strict, mais plus exactement des procédures. Une « vraie » fonction (au sens strict) doit en effet renvoyer une valeur lorsqu’elle se termine. Une « raie » fonction peut s’utiliser à la droite du signe égale dans des expressions telles que :
y = sin(a).
On comprend aisément que dans cette expression, la fonction sin() renvoie une valeur (le sinus de l’argument a qui est directement affectée à la variable y. Commençons par des exemples simples :
Exemple 25 : x est un nombre réel non nul et n un entier naturel.
Exemple 26 : x est un nombre réel non nul et n un entier relatif.
#25calcul
#fonction qui calcule x^n
def exposant(x,n):
p=1
if n>0:
for i in range(n):
p=x*p
return p
resultat=exposant(2,10)
print('2^0= ',resultat)
#26calcul
#fonction qui calcule x^n
#n entier relatif
def exposant(x,n):
p=1
for i in range(n):
p=x*p
return p
def puissance(x,n):
if n>=0:p=exposant(x,n)
if n<0:p=1/exposant(x,-n)
return p
resultat=puissance(2,-3)
print('2^(-3)= ',resultat)
resultat=puissance(-2,3)
print('(-2)^3= ',resultat)
2^0= 1024
2^(-3)= 0.125
(-2)^3= -8
L’instruction return définit ce que doit être la valeur renvoyée par la fonction. En l’occurrence, il s’agit du cube de l’argument qui a été transmis lors de l’appel de la fonction.
LES TABLEAUX
Dans le langage python il faut importer des modules qui contiennent le type array (tableau).
Nous allons procéder sans importer de module, on va utiliser les listes pour créer des tableaux, cela permettra de pouvoir stocker toutes sorte de données dans les tableaux.
Les tableaux servent à stocker des données dans un programme, ils ont l’avantage d’être modifiables et de changer de dimensions selon les besoins du programme.
Nous allons définir des fonctions qui vont créer des tableaux, qui vont remplir des tableaux à partir de listes de données. Ainsi que faire du tri croissant et décroissant.
Création d’un tableau :
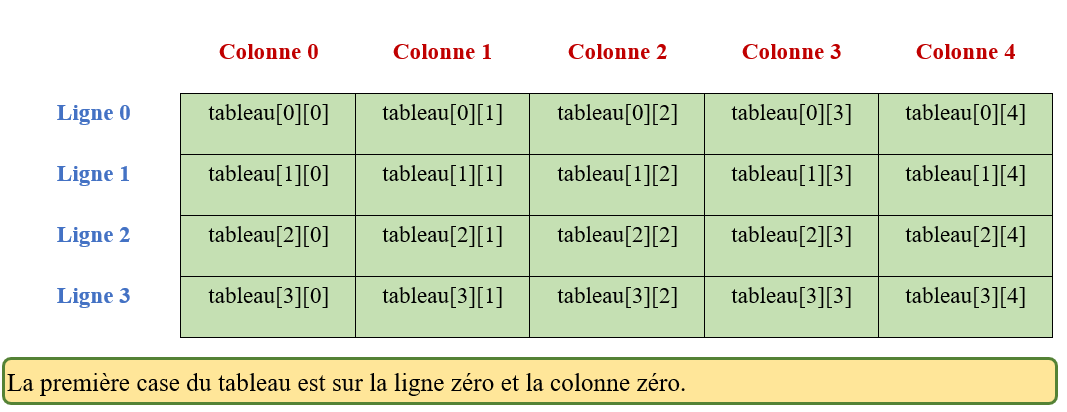
On va créer des tableaux à l’aide d’une fonction qui va prendre en paramètres le nombre de lignes et le nombre de colonnes.
Module tableau:
Ce fichier peut être importé par un autre programme comme un module.
#tableau.py
from random import *
from math import *
def Tableau(ligne,colonne):
#fabrication d'un tableau lignes colonnes
tableau=ligne*[0]
for ln in range(ligne):tableau[ln]=colonne*[0]
return tableau
def remplir(liste,ligne,colonne):
#remplissage du tableau par une liste
tableau=Tableau(ligne,colonne)
for ln in range(0,ligne):
for cn in range(0,colonne):
tableau[ln][cn]=liste[colonne*ln+cn]
return tableau
def liste_neuf(debut):
#fabrique une liste d'entiers de [0,1,2,3,4,5,6,7,8,9]
lst=9*[0]
for i in range(9):
lst[i]=(debut+i)%9+1
return lst
def melange(liste):
# remplissage aléatoire d'une liste de nombres entiers
numimage=len(liste)
for i in range(numimage):liste[i]=2
k=0
while k<numimage-1:
remelange=False
numero=randrange(0,numimage)
for j in range(0,numimage):
if numero==liste[j] :remelange=True
if remelange==False:
liste[k]=numero
k=k+1
return liste
def listetableau(tableau,ligne,colonne):
#fabrication d'une liste avec un tableau lignes colonnes
liste=[]
for ln in range(0,ligne):
for cn in range(0,colonne):
liste.append(tableau[ln][cn])
return liste
def fabrique_liste(taille,nombre):
#construit une liste de taille contenant le nombre
liste=[]
for i in range(taille):liste.append(nombre)
return liste
def cherche(tableau,ligne,colonne,nombre):
#recherche l'emplacement du nombre dans le tableau
for ln in range(0,ligne):
for cn in range(0,colonne):
if tableau[ln][cn]==nombre:
x,y=cn,ln
return x,y# retourne la colonne x et la ligne y
def liste_croissante(liste):
#tri d'une liste en sortie la liste est triée de façon croissante
liste.sort()
return liste
def liste_decroissante(liste):
#tri d'une liste en sortie la liste est triée de façon décroissante
liste.sort()
liste.reverse()
return liste
FONCTION lambda
La fonction lambda est une manière simplifiée d’écrire des fonctions.
>>> lambda x: x\*x*x
>>> <function <lambda> at 0x02E4A420>
>>> f=lambda x:x**3
>>> f(2)
>>> 8
Mais surtout elle permet le passage d’une fonction comme argument. Des
exemples sont donnés dans le chapitre ;
Programme fonctionnel
PGCD
PGCD de deux entiers
Définitions
a et b étant des entiers relatifs, on note D(a) l’ensemble des diviseurs de a , D(b) l’ensemble des diviseurs de b et l’ensemble des diviseurs communs à a et à b .
On a donc :D(a,b) = D(a)∩D(b) .
Note
D(35) = {−35 ; −7 ; −5 ; −1 ;1;5;7;35}
D(6 3) = {−63 ; −21 ; −9 ; −7 ; −3 ; −1;1; 3; 7; 9; 21 ; 63} et donc D(15,63)= {−7 ; −1 ; 1 ; 7}.
On appelle PGCD de a et de b , où a et b sont deux entiers relatifs non tous les deux nuls, le plus grand diviseur commun à a et à b et on le note PGCD(a.b) .
Propriété 1 (Lemme d’Euclide) :
étant deux entiers naturels avec b≠0 et r le reste de la division euclidienne de a par b alors D(a,b) = D(b,r) et donc PGCD(a,b) = PGCD(b,r)
Propriété 2 :
a et b étant deux entiers naturels avec b≠0 , si b divise a alors D(a,b) = D(b) et donc PGD(a;b)=b
Algorithme d’Euclide
Note
Théorème :
a et b sont deux entiers naturels tels que b≠0 . Pour trouver le PGCD(a;b) , on applique l’algorithme suivant appelé algorithme d’Euclide ou algorithme des divisions euclidiennes successives et celui-ci est obtenu en un nombre fini d’étapes :
Calculer le reste r de la division euclidienne de a par b ;
Si r =0 alors PGCD(a;b)=b ;
Si r≠0 alors on remplace a par b et b par r et on recommence à partir de 1).
FONCTION lambda
La fonction lambda est une manière simplifiée d’écrire des fonctions.
;;
>> lambda x: x*x*x
>>> <function <lambda> at 0x02E4A420>
>>> f=lambda x:x**3
>>> f(2)
>>> 8
Mais surtout elle permet le passage d’une fonction comme argument. Des exemples sont donnés dans le chapitre ;
PGCD
PGCD de deux entiers
Définitions
Le PGCD est le plus grand commun diviseur de 2 entiers.
a et b étant des entiers relatifs, on note D(a) l’ensemble des diviseurs de a , D(b) l’ensemble des diviseurs de b et l’ensemble des diviseurs communs à a et à b . On a donc :D(a,b) = D(a)∩D(b) .
Note
D(35) = {−35 ; −7 ; −5 ; −1 ;1;5;7;35}
D(6 3) = {−63 ; −21 ; −9 ; −7 ; −3 ; −1;1; 3; 7; 9; 21 ; 63} et donc D(15,63)= {−7 ; −1 ; 1 ; 7}.
On appelle PGCD de a et de b , où a et b sont deux entiers relatifs non tous les deux nuls, le plus grand diviseur commun à a et à b et on le note PGCD(a.b) .
Propriété 1 (Lemme d’Euclide) :
étant deux entiers naturels avec b≠0 et r le reste de la division euclidienne de a par b alors D(a,b) = D(b,r) et donc PGCD(a,b) = PGCD(b,r)
Propriété 2 :
a et b étant deux entiers naturels avec b≠0 , si b divise a alors D(a,b) = D(b) et donc PGD(a;b)=b
Algorithme d’Euclide
Note
Théorème : a et b sont deux entiers naturels tels que b≠0 . Pour trouver le PGCD(a;b) , on applique l’algorithme suivant appelé algorithme d’Euclide ou algorithme des divisions euclidiennes successives et celui-ci est obtenu en un nombre fini d’étapes :
Calculer le reste r de la division euclidienne de a par b ;
- Si ::
r =0
alors
PGCD(a;b)=b ;
Si r≠0 alors on remplace a par b et b par r et on recommence à partir de 1.
Code des fonctions PGCD
Programme
Résultat
def pgcd(a,b):
return a if b==0 else pgcd(b,a%b)
print('--------PGCD------------')
a=int(input("Donner un nombre entier : "))
b=int(input("Donner un nombre entier : "))
r=pgcd(a,b)
print('PGCD( ', a,' ; ',b,' ) = ', r)
--------PGCD------------
Donner un nombre entier : 456
Donner un nombre entier : 42
PGCD( 456 ; 42 ) = 6
--------PGCD------------
Donner un nombre entier : 79
Donner un nombre entier : 13
PGCD( 79 ; 13 ) = 1
second degré
Programme
Résultat
#second degre.py
def calc_degre2(a,b,c,x):
#Calcul de f(x)=ax²+bx+c
t_f=a*x*x+b*x+c
return t_f
def f_degre2(a,b,c):
#Calcule des coordonnées du sommet de la parabole
if a!=0:
alpha=-b/(2*a)
beta=calc_degre2(a,b,c,alpha)
if a>0:
print("La fonction f admet un minimum m = ",beta)
if a<0:
print("La fonction f admet un maximum M = ",beta)
print("le point S(",alpha," ; ",beta,") est le sommet de la parabole")
continuer=True
#while : tant que
while continuer==True:
print("fonction du second degré: f(x)=ax²+bx+c ")
a1=input("Donner a : ")
try: a=float(a1)
except:a=int(a1)
b1=float(input("Donner b : "))
try: b=float(b1)
except:b=int(b1)
c1=float(input("Donner c : "))
try: c=float(c1)
except:c=int(c1)
f_degre2(a,b,c)
reponse=input("Voulez vous continuer ? (oui/non) : ")
if reponse!='oui':continuer=False
fonction du second degré: f(x)=ax²+bx+c
Donner a : 5
Donner b : 8
Donner c : 10
La fonction f admet un minimum m = 6.8
le point S( -0.8 ; 6.8 ) est le sommet de la parabole
Voulez vous continuer ? (oui/non) :
Calculer le reste r de la division euclidienne de a par b ;
Si r =0 alors PGCD(a;b)=b ;
Si r≠0 alors on remplace a par b et b par r et on recommence à partir de 1).
- Si ::
r =0
Note La programmation est l’art d’apprendre à un ordinateur comment accomplir des tâches qu’il n’était pas capable de réaliser auparavant. L’une des méthodes les plus intéressantes pour y arriver consiste à ajouter de nouvelles instructions au langage de programmation que vous utilisez, sous la forme de fonctions originales.
Définir une fonction
Note
Les scripts que vous avez écrits jusqu’à présent étaient à chaque fois très courts, car leur objectif était seulement de vous faire assimiler les premiers éléments du langage. Lorsque vous commencerez à développer de véritables projets, vous serez confrontés à des problèmes souvent forts complexes, et les lignes de programme vont commencer à s’accumuler… L’approche efficace d’un problème complexe consiste souvent à le décomposer en plusieurs sous-problèmes plus simples qui seront étudiés séparément (ces sous-problèmes peuvent éventuellement être eux-mêmes décomposés à leur tour, et ainsi de suite). D’autre part, il arrivera souvent qu’une même séquence d’instructions doive être utilisée à plusieurs reprises dans un programme.
La syntaxe Python pour la définition d’une fonction est la suivante :
def nom_de_la_fonction(paramètres) :
{indentation} Bloc d’instructions
Vous pouvez choisir n’importe quel nom pour la fonction que vous créez, à l’exception des mots réservés du langage, et à la condition de n’utiliser aucun caractère spécial ou accentué (le caractère souligné » _ » est permis). Comme c’est le cas pour les noms de variables, il vous est conseillé d’utiliser surtout des lettres minuscules, notamment au début du nom (les noms commençant par une majuscule seront réservés aux classes. Comme les instructions if et while que vous connaissez déjà, l’instruction def est une instruction composée. La ligne contenant cette instruction se termine obligatoirement par un double point, lequel introduit un bloc d’instructions que vous ne devez pas oublier d’indenter. La liste de paramètres spécifie quelles informations il faudra fournir en guise d’arguments lorsque l’on voudra utiliser cette fonction (les parenthèses peuvent parfaitement rester vides si la fonction ne nécessite pas d’arguments). Une fonction s’utilise pratiquement comme une instruction quelconque. Dans le corps d’un programme, un appel de fonction est constitué du nom de la fonction suivi de parenthèses. Si c’est nécessaire, on place dans ces parenthèses le ou les arguments que l’on souhaite transmettre à la fonction. Il faudra en principe fournir un argument pour chacun des paramètres spécifiés dans la définition de la fonction, encore qu’il soit possible de définir pour ces paramètres des valeurs par défaut.
Exemple 0501 :
Programme |
Résultat |
|---|---|
#fonction_multiplication.py
# définir une fonction
def table(base):
n=1
while n<10:
print(n,'x',base,'= ',n*base, ' ;')
n=n+1
#programme principal
base=int(input("Entrer un nombre entier :"))
table(base) # appel de la fonction
|
Entrer un nombre entier :5
1 x 5 = 5 ;
2 x 5 = 10 ;
3 x 5 = 15 ;
4 x 5 = 20 ;
5 x 5 = 25 ;
6 x 5 = 30 ;
7 x 5 = 35 ;
8 x 5 = 40 ;
9 x 5 = 45 ;
|
Pour les puristes, les fonctions que nous avons décrites jusqu’à présent ne sont pas tout à fait des fonctions au sens strict, mais plus exactement des procédures. Une « vraie » fonction (au sens strict) doit en effet renvoyer une valeur lorsqu’elle se termine. Une « raie » fonction peut s’utiliser à la droite du signe égale dans des expressions telles que :
y = sin(a).
On comprend aisément que dans cette expression, la fonction sin() renvoie une valeur (le sinus de l’argument a qui est directement affectée à la variable y. Commençons par des exemples simples :
Exemple 25 : x est un nombre réel non nul et n un entier naturel. |
Exemple 26 : x est un nombre réel non nul et n un entier relatif. |
#26calcul
#fonction qui calcule x^n
#n entier relatif
def exposant(x,n):
p=1
for i in range(n):
p=x*p
return p
def puissance(x,n):
if n>=0:p=exposant(x,n)
if n<0:p=1/exposant(x,-n)
return p
resultat=puissance(2,-3)
print('2^(-3)= ',resultat)
resultat=puissance(-2,3)
print('(-2)^3= ',resultat)
|
|---|---|
2^0= 1024
|
2^(-3)= 0.125
(-2)^3= -8
|
L’instruction return définit ce que doit être la valeur renvoyée par la fonction. En l’occurrence, il s’agit du cube de l’argument qui a été transmis lors de l’appel de la fonction.
Dans le langage python il faut importer des modules qui contiennent le type array (tableau). Nous allons procéder sans importer de module, on va utiliser les listes pour créer des tableaux, cela permettra de pouvoir stocker toutes sorte de données dans les tableaux. Les tableaux servent à stocker des données dans un programme, ils ont l’avantage d’être modifiables et de changer de dimensions selon les besoins du programme. Nous allons définir des fonctions qui vont créer des tableaux, qui vont remplir des tableaux à partir de listes de données. Ainsi que faire du tri croissant et décroissant.
Création d’un tableau : On va créer des tableaux à l’aide d’une fonction qui va prendre en paramètres le nombre de lignes et le nombre de colonnes.
Module tableau:
Ce fichier peut être importé par un autre programme comme un module.
#tableau.py
from random import *
from math import *
def Tableau(ligne,colonne):
#fabrication d'un tableau lignes colonnes
tableau=ligne*[0]
for ln in range(ligne):tableau[ln]=colonne*[0]
return tableau
def remplir(liste,ligne,colonne):
#remplissage du tableau par une liste
tableau=Tableau(ligne,colonne)
for ln in range(0,ligne):
for cn in range(0,colonne):
tableau[ln][cn]=liste[colonne*ln+cn]
return tableau
def liste_neuf(debut):
#fabrique une liste d'entiers de [0,1,2,3,4,5,6,7,8,9]
lst=9*[0]
for i in range(9):
lst[i]=(debut+i)%9+1
return lst
def melange(liste):
# remplissage aléatoire d'une liste de nombres entiers
numimage=len(liste)
for i in range(numimage):liste[i]=2
k=0
while k<numimage-1:
remelange=False
numero=randrange(0,numimage)
for j in range(0,numimage):
if numero==liste[j] :remelange=True
if remelange==False:
liste[k]=numero
k=k+1
return liste
def listetableau(tableau,ligne,colonne):
#fabrication d'une liste avec un tableau lignes colonnes
liste=[]
for ln in range(0,ligne):
for cn in range(0,colonne):
liste.append(tableau[ln][cn])
return liste
def fabrique_liste(taille,nombre):
#construit une liste de taille contenant le nombre
liste=[]
for i in range(taille):liste.append(nombre)
return liste
def cherche(tableau,ligne,colonne,nombre):
#recherche l'emplacement du nombre dans le tableau
for ln in range(0,ligne):
for cn in range(0,colonne):
if tableau[ln][cn]==nombre:
x,y=cn,ln
return x,y# retourne la colonne x et la ligne y
def liste_croissante(liste):
#tri d'une liste en sortie la liste est triée de façon croissante
liste.sort()
return liste
def liste_decroissante(liste):
#tri d'une liste en sortie la liste est triée de façon décroissante
liste.sort()
liste.reverse()
return liste
|
|---|
La fonction lambda est une manière simplifiée d’écrire des fonctions.
Mais surtout elle permet le passage d’une fonction comme argument. Des exemples sont donnés dans le chapitre ;
PGCD de deux entiers
Définitions
a et b étant des entiers relatifs, on note D(a) l’ensemble des diviseurs de a , D(b) l’ensemble des diviseurs de b et l’ensemble des diviseurs communs à a et à b . On a donc :D(a,b) = D(a)∩D(b) .
Note
D(35) = {−35 ; −7 ; −5 ; −1 ;1;5;7;35}
D(6 3) = {−63 ; −21 ; −9 ; −7 ; −3 ; −1;1; 3; 7; 9; 21 ; 63} et donc D(15,63)= {−7 ; −1 ; 1 ; 7}.
On appelle PGCD de a et de b , où a et b sont deux entiers relatifs non tous les deux nuls, le plus grand diviseur commun à a et à b et on le note PGCD(a.b) .
Propriété 1 (Lemme d’Euclide) :
étant deux entiers naturels avec b≠0 et r le reste de la division euclidienne de a par b alors D(a,b) = D(b,r) et donc PGCD(a,b) = PGCD(b,r)
Propriété 2 :
a et b étant deux entiers naturels avec b≠0 , si b divise a alors D(a,b) = D(b) et donc PGD(a;b)=b
Algorithme d’Euclide
Note
Théorème : a et b sont deux entiers naturels tels que b≠0 . Pour trouver le PGCD(a;b) , on applique l’algorithme suivant appelé algorithme d’Euclide ou algorithme des divisions euclidiennes successives et celui-ci est obtenu en un nombre fini d’étapes :
La fonction lambda est une manière simplifiée d’écrire des fonctions.
;;
>> lambda x: x*x*x >>> <function <lambda> at 0x02E4A420> >>> f=lambda x:x**3 >>> f(2) >>> 8
Mais surtout elle permet le passage d’une fonction comme argument. Des exemples sont donnés dans le chapitre ;
PGCD de deux entiers Définitions Le PGCD est le plus grand commun diviseur de 2 entiers. a et b étant des entiers relatifs, on note D(a) l’ensemble des diviseurs de a , D(b) l’ensemble des diviseurs de b et l’ensemble des diviseurs communs à a et à b . On a donc :D(a,b) = D(a)∩D(b) .
Note
D(35) = {−35 ; −7 ; −5 ; −1 ;1;5;7;35}
D(6 3) = {−63 ; −21 ; −9 ; −7 ; −3 ; −1;1; 3; 7; 9; 21 ; 63} et donc D(15,63)= {−7 ; −1 ; 1 ; 7}.
On appelle PGCD de a et de b , où a et b sont deux entiers relatifs non tous les deux nuls, le plus grand diviseur commun à a et à b et on le note PGCD(a.b) .
Propriété 1 (Lemme d’Euclide) : étant deux entiers naturels avec b≠0 et r le reste de la division euclidienne de a par b alors D(a,b) = D(b,r) et donc PGCD(a,b) = PGCD(b,r)
Propriété 2 : a et b étant deux entiers naturels avec b≠0 , si b divise a alors D(a,b) = D(b) et donc PGD(a;b)=b
Algorithme d’Euclide Note
Théorème : a et b sont deux entiers naturels tels que b≠0 . Pour trouver le PGCD(a;b) , on applique l’algorithme suivant appelé algorithme d’Euclide ou algorithme des divisions euclidiennes successives et celui-ci est obtenu en un nombre fini d’étapes :
Calculer le reste r de la division euclidienne de a par b ;
alors
PGCD(a;b)=b ;
Si r≠0 alors on remplace a par b et b par r et on recommence à partir de 1.
Code des fonctions PGCD
Programme |
Résultat |
|---|---|
def pgcd(a,b):
return a if b==0 else pgcd(b,a%b)
print('--------PGCD------------')
a=int(input("Donner un nombre entier : "))
b=int(input("Donner un nombre entier : "))
r=pgcd(a,b)
print('PGCD( ', a,' ; ',b,' ) = ', r)
|
--------PGCD------------
Donner un nombre entier : 456
Donner un nombre entier : 42
PGCD( 456 ; 42 ) = 6
--------PGCD------------
Donner un nombre entier : 79
Donner un nombre entier : 13
PGCD( 79 ; 13 ) = 1
|
Programme |
Résultat |
|---|---|
#second degre.py
def calc_degre2(a,b,c,x):
#Calcul de f(x)=ax²+bx+c
t_f=a*x*x+b*x+c
return t_f
def f_degre2(a,b,c):
#Calcule des coordonnées du sommet de la parabole
if a!=0:
alpha=-b/(2*a)
beta=calc_degre2(a,b,c,alpha)
if a>0:
print("La fonction f admet un minimum m = ",beta)
if a<0:
print("La fonction f admet un maximum M = ",beta)
print("le point S(",alpha," ; ",beta,") est le sommet de la parabole")
continuer=True
#while : tant que
while continuer==True:
print("fonction du second degré: f(x)=ax²+bx+c ")
a1=input("Donner a : ")
try: a=float(a1)
except:a=int(a1)
b1=float(input("Donner b : "))
try: b=float(b1)
except:b=int(b1)
c1=float(input("Donner c : "))
try: c=float(c1)
except:c=int(c1)
f_degre2(a,b,c)
reponse=input("Voulez vous continuer ? (oui/non) : ")
if reponse!='oui':continuer=False
|
fonction du second degré: f(x)=ax²+bx+c
Donner a : 5
Donner b : 8
Donner c : 10
La fonction f admet un minimum m = 6.8
le point S( -0.8 ; 6.8 ) est le sommet de la parabole
Voulez vous continuer ? (oui/non) :
|