_frame/icon.png

Introduction

.

Exercice N°1 :

.

Enoncé arbre

Dans cet exercice, un arbre binaire de caractères est stocké sous la forme d’un
dictionnaire où les clefs sont les caractères des nœuds de l’arbre et les valeurs, pour
chaque clef, la liste des caractères des fils gauche et droit du nœud.
Par exemple, l’arbre

est stocké dans un dictionnaire

 

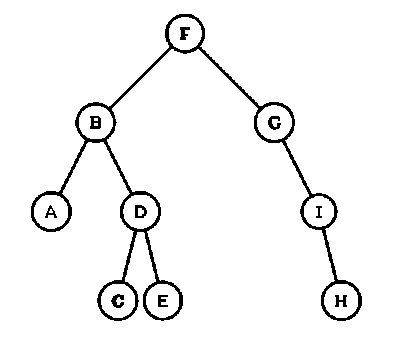
a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'],'C':['',''], 'E':['',''],\  'G':['','I'], 'I':['','H'], 'H':['','']}

 

Écrire une fonction récursive taille prenant en paramètres un arbre binaire arbre sous la forme d’un dictionnaire et un caractère lettre qui est la valeur du sommet de  l’arbre, et qui renvoie la taille de l’arbre à savoir le nombre total de nœud. On pourra distinguer les 4 cas où les deux « fils » du nœud sont '', le fils gauche seulement est '', le fils droit seulement est '', aucun des deux fils n’est ''.
Exemple :

 

>>> taille(a,'F')

9
image/29.png

Réponse 

 

a = {'F':['B','G'], 'B':['A','D'], 'A':['',''], 'D':['C','E'], \

'C':['',''], 'E':['',''], 'G':['','I'], 'I':['','H'], \

'H':['','']}

k=0

def taille(a,s):

    global k

    if s in a:

        k=k+1  

        if a[s][0]!='':        

            taille(a,a[s][0])

        if a[s][1]!='':   

            taille(a,a[s][1])              

        else: k=k

        return k  

.

Exercice N°2 :

.

Chercher :

 

On considère l'algorithme de tri de tableau suivant : à chaque étape, on parcourt depuis
le début du tableau tous les éléments non rangés et on place en dernière position le plus
grand élément.

 

Exemple avec le tableau :

 

t =[41, 55, 21, 18, 12, 6, 25]

 

Etape 1 :

On parcourt tous les éléments du tableau, on permute le plus grand élément avec le dernier. Le tableau devient

t =[41, 25, 21, 18, 12, 6, 55]

 

Etape 2 : on parcourt tous les éléments sauf le dernier, on permute le plus grand élément
trouvé avec l'avant dernier. Le tableau devient :
t = [6, 25, 21, 18, 12, 41, 55]
Et ainsi de suite.
La code de la fonction tri_iteratif qui implémente cet algorithme est donné ci-dessous.

Question :

def tri_iteratif(tab):

    for k in range( ... , 0, -1):

        imax = ...

        for i in range(0 , ... ):

            if tab[i] > ... :

                imax = i

        if tab[max] > ... :

            ... , tab[imax] = tab[imax] , ...

    return tab

chercher

Compléter le code qui doit donner :

 

>>> tri_iteratif([41, 55, 21, 18, 12, 6, 25])

[6, 18, 12, 21, 25, 41, 55]

 

On rappelle que l’instruction
a, b = b, a
échange les contenus de a et de b.

.

REPONSE

.

Programme 

tab =[41, 55, 21, 18, 12, 6, 25]

def tri_iteratif(tab):  

    for k in range( (len(tab)-1) , 0, -1):      

        imax =k

        for i in range(0 ,k):  

            if tab[i] >tab[imax]:             

                imax=i   

            if tab[imax] > tab[k]:

                tab[k], tab[imax] = tab[imax] ,tab[k]

    return tab

Il faut utiliser idle et copier la commande ci-dessous et appuyer sur entrée

>>> tri_iteratif([41, 55, 21, 18, 12, 6, 25])