Codage des nombres :
- Introduction
- Représentation des entiers naturels
- Représentation des entiers relatifs
- Représentation des nombres réels
- Exemples : Binaire, hexadécimal en python
.
Introduction :
Les ordinateurs et les programmes que l’on utilise tous les jours permettent de mémoriser, de transmettre et de transformer des nombres, des textes, des images, des sons, etc.
Pourtant, ces ordinateurs ne manipulent que des objets simples : des 0 et des 1.
Mémoriser, transmettre et transformer des nombres, des textes, des images ou des sons demande donc d’abord de les représenter comme des suites de 0 et de 1.
Une telle valeur, 0 ou 1, s’appelle un booléen, un chiffre binaire ou encore un bit (binary digit). Un tel circuit à deux états s’appelle un circuit mémoire un bit et son état se décrit donc par le symbole 0 ou par le symbole 1.
Numération de position :
La valeur d’un chiffre dépend de sa position et de la base :
Base 10 (décimale) :
Notation décimale par position
Dix chiffres sont nécessaires : \(0~;1~;2~;3~;4~;5~;6~;7~;8~;9~;\)
Vocabulaire :
10 est une dizaine. 100 est une centaine. 1000 est un millier ………….
Exemple :
| \(nombre\,\,\, =\) | \(les\,\,\, milliers\,\,\, +\) | \(les,\,\, centaines\,\, +\) | \(les\ ,\,\,\, dizaines\,\,\,+\) | \(les\ ,\,\,\ unité s\) |
| Position | 3 | 2 | 1 | 0 |
| \(nombre\,\,\, =\) | \(3\,\,\, milliers\,\,\,\, +\) | \(7\,\,\, centaines\,\,\,\,+\) | \(4\,\,\, dizaines\,\,\,\, +\) | \(5\,\ , unités\) |
| \(~~3745\,\,\, =\) | \(3 \times 10^{3} \,\, +\) | \(7 \times 10^{2}\,\, +\) | \(4 \times 10^{1}\,\,\, +\) | \(5 \times 10^{0}\) |
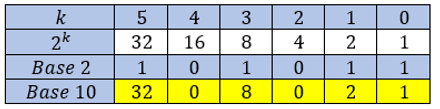
Base 2 (binaire) :
Notation binaire par position.
Deux chiffres sont nécessaires : .
Vocabulaire :
2 est une deuzaine. 4 est une quatraine. 8 est une huitaine. 16 est une sezaine. 32 est une trente-deuzaine …
Exemple :
| Positions | 4 | 3 | 2 | 1 | 0 |
| Valeur
binaire = 11011 |
1 | 1 | 0 | 1 | 1 |
| Exposants | \(2^{4}\) | \(2^{3}\) | 0 | \(2^{1}\) | 1 |
| Valeur
décimale = 27 |
16 | 8 | 0 | 2 | 1 |
.
Représentation des entiers relatifs
Il existe deux conventions pour représenter les nombres entiers relatifs en notation binaire.
La convention dite : « Par complément à \(\mathbf{2}^{\mathbf{n}}\) »
La convention dite : « Par bit de signe »
“n” étant le nombre de bits du format utilisé. La convention par “complément à \(2^{n}\) ” est parfois improprement nommée “Complément à 2”
Cette méthode permet d’utiliser les opérations classiques sans problème.
Définition
On nomme « Complément à 1 » d’un nombre binaire Le nombre obtenu en remplaçant tous ses ‘1’ par des zéros et tous ses zéros par des ‘1’.
Exemple 1:
N = 0 1 1 0 1 0 1 et ~N = 1 0 0 1 0 1 0
En symbolisant “Complément à 1 de N ” par ~N
Exemple 2:
huit bits : \(2^{7}=127\). l'entier relatif est compris entre 0 et 127
Représentation binaire sur huit bits de l'entier relatif 4:
L'entier relatif 4 est représenté comme l'entier naturel 4 = 0000 0100.
Pour calculer la représentation de son opposé, on remplace les 0 par 1 et les 1 par des 0, ce qui donne 1111 1011.
4= 0000 0100 et ~4 = 1111 10111
L'opposé de 4 est calculé par la formule : -4 = ~4 + 1 . C'est à dire -4 = 1111 1011 + 0000 0001 = 1111 1100
1111 1100 = 1000 0000 - 0000 0100 ce qui signifie 252 = 256 - 4
La convention :
- Un nombre binaire sera positif si son premier bit à gauche, (le bit le plus signifiant : MSB ) est “0”,Les nombres positifs ont un MSB = 0 et les négatifs MBS=1
Définition :
· l’opposé d’un nombre N sera : \(\left. - \mathbf{N}\ = \ \right.\sim\mathbf{N}\ + \ \mathbf{1}\)
Exemple :
\(\begin{array}{l} {~\boxed{\begin{array}{l} {\,\,\,\,\,\,\,\, N\ = \ 0 0 1 1 0 1 1 0\ \left( {base 10\ :\ + 54} \right)~~} \\ {\sim N\ = \ 1 1 0 0 1 0 0 1~~~~~~~~~~~~~~\ ~~\,\,\,\,\,~~ + \ 1~~~~} \\ \end{array}}} \\ {~~~ - N\ = \,\,~1 1 0 0 1 0 1 0~~\left( {base 10\ :\ - 54} \right)} \\ \end{array}\)
.
Représentation des nombres réels
Définition :
Un nombre est représenté sous la forme \(s m 2^{n}\) où \(s\) est le signe nombre, \( n\) son exposant on le représente comme l'entier naturel \(n + 1023 \) si \(n + 1 023 \) et \(m \) sa mantisse
Quand on utilise 64 bits pour représenter un nombre à virgule, on utilise 1 bit pour le signe, 11 bits pour l'exposant et 52 bits pour la mantissse. Le signe + est représenté par 0 et le signe - par 1. L'exposant est un entier relatif compris entre \(-1 022\) et \(1 023\)
Exemple :
Représentation d'un nombre réel en binaire : 110001000110100100111100001110000000000000000000000000000000000
1 est le signe : - 10001000110 est égal à 1 094 = n + 1023, donc n = 1094 - 1023 = 71 100100111100001110000000000000000000000000000000000 est la mantisse m
m = 1. 1001 0011 1100 0011 1000 0000 0000 0000 0000 0000 0000 0000 0000
1.1001 0011 1100 0011 1 = \(\frac{1}{2^{1}}+\frac{1}{2^{4}} + \frac{1}{2^{7}} + \frac{1}{2^{8}} + \frac{1}{2^{9}} + \frac{1}{2^{10}} + \frac{1}{2^{15}} + \frac{1}{2^{16}} + \frac{1}{2^{17}}\)
Définition :
Pour tout nombre binaire représentant un réel :
Exemple du calcul d'un nombre à virgule : traduire en binaire le nombre qui est en base 10
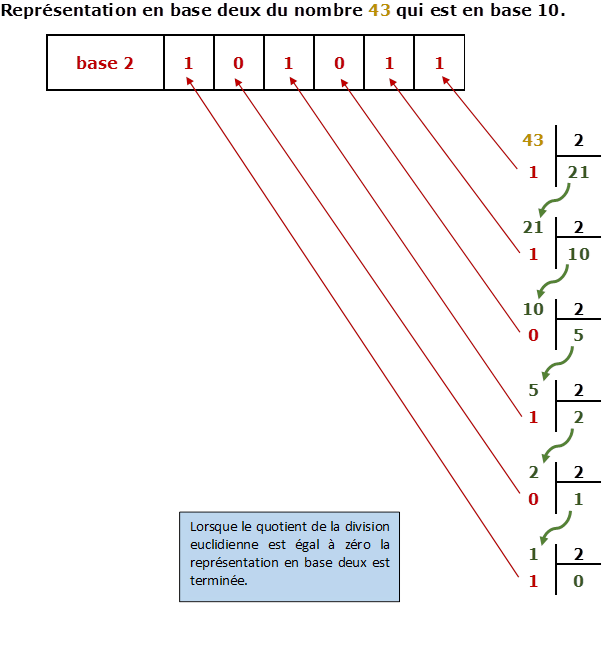
.
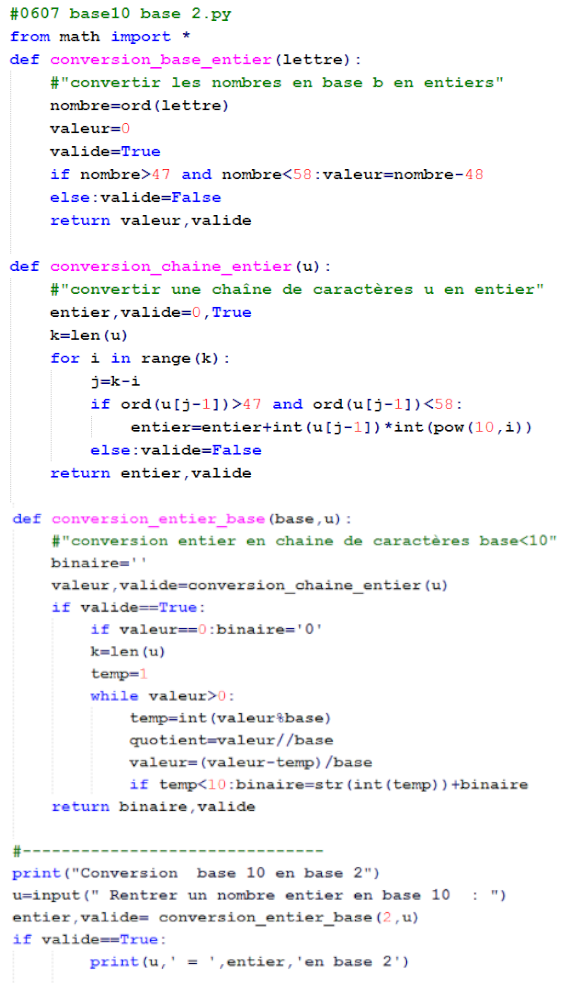
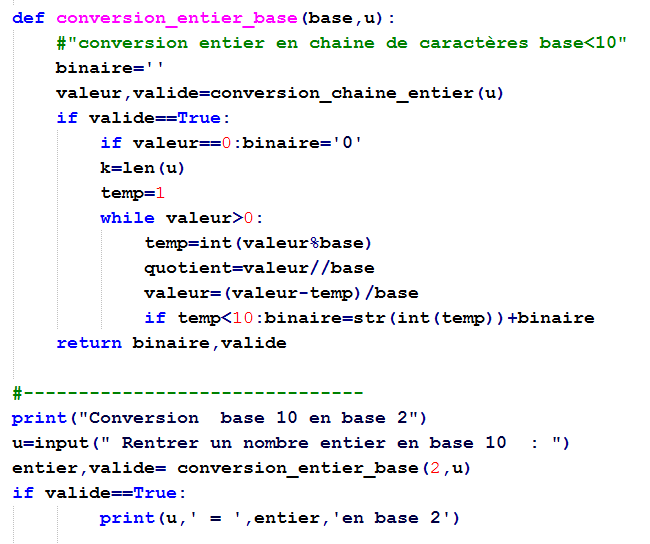
Exemples :
Changer la représentation d’un nombre entier :
On écrit les nombres entiers naturels en notation décimale à position. C’est-à-dire que le nombre \(\ 458 = 4 \times 10^{2} + 5 \times 10^{1} + \ 8 \times 10^{0} = 400 + 50 + 8\).
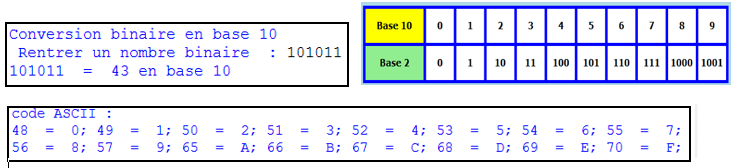
Binaire :
En base 2 le nombre 101011 est égal en base 10 à : \(32 + 8 + 2 + 1 = 43\)
.
.
.
.
.
Hexadécimal :
.
Résultat :