mathematiques

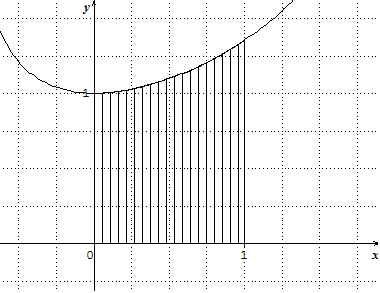
Méthode des rectangles

.

TP énoncé
Algorithme
Code final
Module math
Module pylab

.

TP : Méthode des rectangles.

.

\[I = \int_{0}^{1}{\frac{e^{x}}{1 + x}\text{dx}}\]

Principe :

On approche la valeur de l’intégrale par l’aire de rectangles dont on diminue la largeur pour augmenter la précision du résultat obtenu.

Mise en application :

On considère la fonction $\text{f }$ définie sur $\lbrack 0\ ;1\rbrack$ par :

\[f\left( x \right) = \frac{e^{x}}{1 + x}\]

Etudier les variations de $\text{f }$ sur $\lbrack 0\ ;1\rbrack\ $;
Pour tout entier $n \geq 1$ , on pose

\[S_{n} = \sum_{k = 0}^{n - 1}{\frac{1}{n} \times f\left( \frac{k}{n} \right)}\text{et }T_{n} = \sum_{k = 1}^{n}{\frac{1}{n} \times f\left( \frac{k + 1}{n} \right)}\]

Justifier que, pour tout entier $k$ de $0$ à:math:n - 1, on a :

\[\frac{1}{n} \times f\left( \frac{k}{n} \right) \leq \int_{\frac{k}{n}}^{\frac{k + 1}{n}}{f(x)dx \leq \frac{1}{n} \times f\left( \frac{k + 1}{n} \right)}\]

b) En déduire que : $S_{n} \leq \int_{0}^{1}{\frac{e^{x}}{1 + x}\text{dx}} \leq T_{n}$

Calculer $T_{n} - S_{n}$

$\frac{1}{n} \times f\left( \frac{k}{n} \right)$ est l’aire d’un rectangle de largeur $\frac{1}{n}$ et de longueur $f\left( \frac{k}{n} \right)$.

On découpe ainsi l’aire sous la courbe en rectangles aussi petits que l’on veut.

.

TP : Algorithme.

.

Ancien Algorithme

Variables :

$n,k$ : entiers ;

$s$ : réel ;

Début

Entrer(n) ;

$S \longleftarrow 0$ ;

Pour $\text{k }$allant de $0$ à $n - 1$ Faire

$S \longleftarrow S + \frac{1}{n} \times f\left( \frac{k}{n} \right)$

FinPour

Afficher ($S$) ;

Fin

Nouvel Algorithme .

Fonction

$f_{n}( k ) =\frac{1}{n} \times\frac{e^{\frac{k}{n}}}{1 + \frac{k}{n}}$

$S \longleftarrow 0$ ;

Pour $\text{k }$allant de $0$ à $n - 1$

$S \longleftarrow S + f_{n}( k )$

Fin Pour

Quel est le résultat final affiché par cet algorithme ?

.

TP : Code final. Module math

.

$math/methode_rectangle01.PNG$

.

TP : Code final. Module pylab

.

$math/methode_rectangle02.PNG$

.

$math/methode_rectangle03.PNG$