Convertion d'entiers naturels dans différentes bases
Codage des nombres entiers :
- Introduction :
- Représentation des entiers naturels
- Code python conversion d’un nombre
- Vidéo de conversion hexadécimal, base 10
- Code python de conversion hexadécimal, base 10
.
Introduction :
.
Les ordinateurs et les programmes que l’on utilise tous les jours permettent de mémoriser, de transmettre et de transformer des nombres, des textes, des images, des sons, etc.
Pourtant, ces ordinateurs ne manipulent que des objets simples : des 0 et des 1.
Mémoriser, transmettre et transformer des nombres, des textes, des images ou des sons demande donc d’abord de les représenter comme des suites de 0 et de 1.
Une telle valeur, 0 ou 1, s’appelle un booléen, un chiffre binaire ou encore un bit (binary digit). Un tel circuit à deux états s’appelle un circuit mémoire un bit et son état se décrit donc par le symbole 0 ou par le symbole 1.
.
Représentation des entiers naturels
.
.
Nombres entiers base 10 :
.
Le système décimal prend 10 pour base et utilise les chiffres : 0 ;1 ;2 ;3 ;4 ;5 ;6 ;7 ;8 ;9 ;
Les entiers naturels sont écrits en notation décimale à position. Il y a une infinité d’entiers naturels (n est une variable qui est utilisé en mathématique pour désigner un entier naturel par exemple pour les suites numériques)
.
Numération de position :
.
La valeur d’un chiffre dépend de sa position et de la base :
\(Valeur = chiffre \times Base^{position\,\,}\,\,\,:\,\,\)
\(345 = 3~ \times 10^{2} + 4 \times ~10^{1} + 5 \times 10^{0}\) : la base est 10.
Le chiffre 3 a pour position 2, le nombre 4 a pour position 1, le nombre 5 a pour position 0.
Vocabulaire :
10 est une dizaine. 100 est une centaine. 1000 est un millier ………….
Exemple :
| \(nombre\,\,\, =\) | \(les\,\,\, milliers\,\,\, +\) | \(les\,\,\, centaines\,\, +\) | \(les\,\,\,\, dizaines\,\,\,+\) | \(les\,\,\, unité s\) |
| Position | 3 | 2 | 1 | 0 |
| \(nombre\,\,\,\ =\) | \(3\,\,\, milliers\,\,\,\, +\) | \(7\,\,\, centaines\,\,\,\,+\) | \(4\,\,\, dizaines\,\,\,\, +\) | \(5\,\, unités\) |
| \(~~3745\,\,\, =\) | \(3 \times 10^{3}\,\, +\) | \(7 \times 10^{2}\,\, +\) | \(4 \times 10^{1}\,\,\, +\) | \(5 \times 10^{0}\) |
.
Base 2 (binaire) :
.
.
Notation binaire par position
.
Deux chiffres sont nécessaires :\(0\ et\ 1\) .
Vocabulaire :
2 est une deuzaine. 4 est une quatraine. 8 est une huitaine. 16 est une sezaine. 32 est une trente-deuzaine …
Exemple :
| Positions | 4 | 3 | 2 | 1 | 0 |
| Valeur binaire =11011 | 1 | 1 | 0 | 1 | 1 |
| Exposants | \(2^{4}\) | \(2^{3}\) | 0 | \(2^{1}\) | 1 |
| Valeur décimale = 27 | 16 | 8 | 0 | 2 | 1 |
.
Base Hexadécimale (base 16) :
.
Pour compter en base 16, on utilise les dix chiffres de la base 10 et on ajoute six lettres A; B; C; D ; E; F.
| Base 16 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Base 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Exemple :
\(1A_{16} = 1 \times 16 + 10 = 26_{10}\)
On écrit les nombres entiers naturels en notation décimale à position.
C’est-à-dire que le nombre\(~458 = 4 \times 10^{2} + 5 \times 10^{1} + ~8 \times 10^{0} = 400 + 50 + 8\).
.
Binaire
.
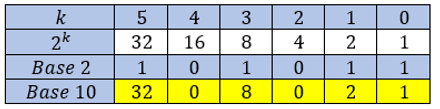
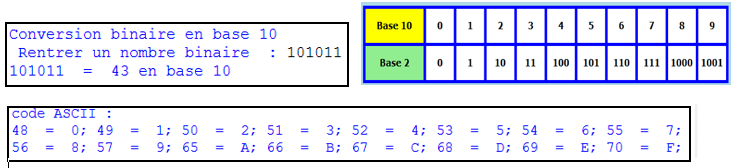
En base 2, le nombre 101011 est égal en base 10 à :
\(32 + 8 + 2 + 1 = 43\)
| \(k\) | \(5\) | \(4\) | \(3\) | \(2\) | \(1\) | \(0\) |
| \(2^{k}\) | \(32\) | \(16\) | \(8\) | \(4\) | \(2\) | \(1\) |
| \(Base~2\) | \(1\) | \(0\) | \(1\) | \(0\) | \(1\) | \(1\) |
| \(Base~10\) | \(32\) | \(0\) | \(8\) | \(0\) | \(2\) | \(1\) |
.
Hexadécimal :
.
En base16 le nombre 7050A1 est égal en base 10 à :
\(7 \times 16^{5} + 5 \times 10^{3} + 160 + 1\)
| \(k\) | \(5\) | \(4\) | \(3\) | \(2\) | \(1\) | \(0\) |
| \(16^{k}\) | \(1048576\) | \(65536\) | \(4096\) | \(256\) | \(16\) | \(1\) |
| \(Base~16\) | \(7\) | \(0\) | \(5\) | \(0\) | \(A\) | \(1\) |
| \(Base~10\) | \(7340032\) | \(0\) | \(20480\) | \(0\) | \(160\) | \(1\) |
.
Conversion d’un nombre dans une base b
.
.
Méthode
.
|
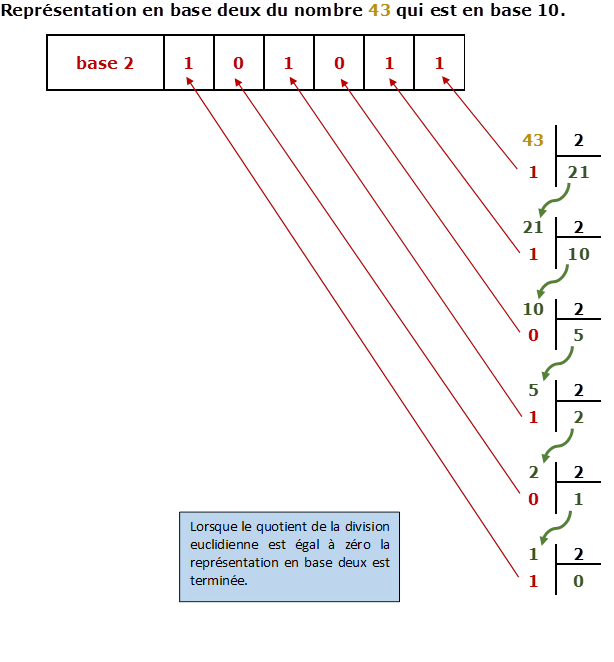
Pour convertir un nombre dans une base b, on le convertit dans la base 10 puis on effectue une division euclidienne par b et la reste de cette division est placé en position zéro dans la base b. Si le quotient est non nul on effectue une division euclidienne du quotient par b le reste est placé en position 1 dans la base b, et si le quotient est non nul on recommence. La conversion se termine quand le quotient est égal à zéro.
.Exemple de conversion. |
 |
.
Code python conversion d’un nombre
.
- Exemples : Binaire, hexadécimal en python
- Vidéo de conversion hexadécimal, base 10
- Code python de conversion hexadécimal, base 10
.
Exemples :
.
|
Changer la représentation d’un nombre entier : On écrit les nombres entiers naturels en notation décimale à position. C’est-à-dire que le nombre\(\ 458 = 4 \times 10^{2} + 5 \times 10^{1} + \ 8 \times 10^{0} = 400 + 50 + 8\). Binaire : En base 2 le nombre 101011 est égal en base 10 à : \(32 + 8 + 2 + 1 = 43\) |
#0607 binaire base10.py
from math import *
def conversion_binaire_base10(lettre):
#"convertir un nombre binaire en entier de base 10"
nombre=ord(lettre)
valeur=0
valide=True
if nombre>47 and nombre<50:valeur=nombre-48
else:valide=False
return valeur,valide
def conversion_binaire(u):
# convertir une chaine de caractères en entiers de base 10
k,entier=len(u),0
valide=True
for i in range(k):
j=k-i
vt,nbr=conversion_binaire_base10(u[j-1])
if nbr==True:
entier=entier+(vt)*int(pow(2,i))
else:valide=False
return entier,valide
#-------------------
print("Conversion binaire en base 10 ")
u=input(" Rentrer un nombre binaire : ")
entier,valide= conversion_binaire(u)
if valide==True:
print(u,' = ',entier,'en base 10')
|
.
Hexadécimal :
.
Résultat :