Nombres Réels
- Représentation des nombres réels en binaire
- Nombre binaire représentant un nombre réel
- Exemple du calcul inverse
- addition
- soustraction
- multiplication
- division
- Représentation approximative
.
Représentation des nombres réels en binaire
.
Définition :
(nombre réel est en base 10)
13, 625 est un nombre réel, il est en base 10. On peut le représenter de
cette façon :
\(13,625 = 1 \times 10 + 3 + \frac{6}{10^{1}} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)
Soit les nombres entiers (ou représentants d’une base supérieure à 10)
\(a_{0};a_{1};...;a_{n}\) et \(b_{0};b_{1};...;b_{m}\) qui
sont compris entre 0 et \(p - 1\) , \(p\) est la valeur de
la base.
On veut écrire un nombre décimal sous la même forme que le
réel \(13,325\) :
\(\left( {a_{n}...a_{0},b_{1}....b_{m}} \right)_{p} = \left( {a_{n} \times p^{n} + ... + a_{0} + \frac{b_{1}}{p} + ... + \frac{b_{m}}{p^{m}}} \right)_{10}\)
.
Exemple
Si on utilise une base supérieure à 10 on remplace A par 10 et B par 11 …
Position
\(3\)
\(2\)
\(1\)
\(0\)
\(- 1\)
\(- 2\)
\(- 3\)
binaire
1
1
0
1
1
0
1
1101,101
Exposant
\(2^{3}\)
\(2^{2}\)
0
\(2^{0}\)
\(\frac{1}{2^{1}} =2^{-1}\)
\(\frac{0}{2^{2}} = 0\)
\(\frac{1}{2^{3}} =2^{-3}\)
Base 10
8
4
0
1
\(\frac{1}{2}\)
0
\(\frac{1}{8}\)
\(\left( {8 + 4} \right),\left( {1 + \frac{1}{2} + \frac{1}{8}} \right) = 12 + \frac{8 + 4 + 1}{8} = 13,625\)
.
Exemple du calcul inverse :
traduire en binaire le nombre\(43,625\) qui est en base 10 :
Pout 43 on divise par 2 le reste est 1 et le quotient est 21 et on
continue pour arriver à un quotient égal à 0.
43=2\(\times\) 21+1
21=2\(\times\) 10+1
10=2\(\times\) 5+0
5=2\(\times\) 2+1
2=2\(\times\) 1+0
1=2\(\times\) 0+1
\(0,625 \times 2 = 1,250 \geq 1\) , on obtient 0,1
\(0.250 \times 2 = 0,500 < 1\) ,on obtient 0,10
\(0,500 \times 2 = 1,000 \geq 1\) , on obtient 0,101
Le nombre décimal 43,625 est égal à 101011,101 en binaire.
.
Opérations
.
Addition
En binaire exemple d’addition
\(\left( 101 \right)_{2} + \left( 11 \right)_{2} = \left( 1000 \right)_{2}\,\,\) (en base 10) on obtient \(5 + 3 = 8\)
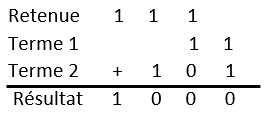
.
Soustraction
En binaire exemple de soustraction \(\left( 101 \right)_{2} - \left( 11 \right)_{2} = \left( 10\right)_{2}\,\,\) (en base 10) on obtient \(5 - 3 = 2\)
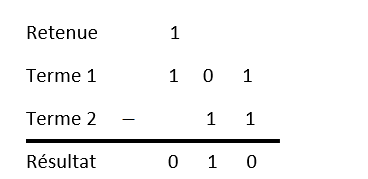
.
Multiplication
En binaire une multiplication est de cette forme \(1 0 1 \times 1 1= 1 1 1 1\) (en base 10) on obtient \(5 \times \ 3=15\)
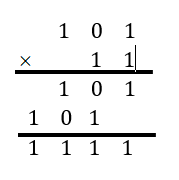
.
Division
En base 2 voici la division \(\frac{110}{11}=10\) : (en base 10 on obtient \(\frac{6}{3}=2\) )
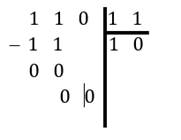
.
Représentation approximative
Précision et arrondi
En base 10 on a comme valeur approchée ou arrondie \(\frac{1}{3}=0,3333....\)
En binaire si on calcule un nombre rationnel on ne peut pas toujours
trouver sa valeur exacte :
.
Par exemple :
\(\\\frac{1}{11}\approx 0, 0 1 0 1.\) et 0, 0 1 0 1 \(=0+\frac{1}{{{2}^{2}}}+\frac{1}{{{2}^{4}}}=\frac{1}{4}+\frac{1}{16}=\frac{5}{16}\approx0,3\)
Si on continue : \(0,0101010101=\frac{1}{{{2}^{2}}}+\frac{1}{{{2}^{4}}}+\frac{1}{{{2}^{6}}}+\frac{1}{{{2}^{8}}}+\frac{1}{{{2}^{10}}}=\frac{314}{1024}\approx0,333\)
- Représentation des nombres réels en binaire
- Nombre binaire représentant un nombre réel
- Exemple du calcul inverse
- addition
- soustraction
- multiplication
- division
- Représentation approximative
.
Représentation des nombres réels en binaire
.
Définition :
(nombre réel est en base 10)
13, 625 est un nombre réel, il est en base 10. On peut le représenter de cette façon :
\(13,625 = 1 \times 10 + 3 + \frac{6}{10^{1}} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)
Soit les nombres entiers (ou représentants d’une base supérieure à 10)
\(a_{0};a_{1};...;a_{n}\) et \(b_{0};b_{1};...;b_{m}\) qui sont compris entre 0 et \(p - 1\) , \(p\) est la valeur de la base.
On veut écrire un nombre décimal sous la même forme que le réel \(13,325\) :
\(\left( {a_{n}...a_{0},b_{1}....b_{m}} \right)_{p} = \left( {a_{n} \times p^{n} + ... + a_{0} + \frac{b_{1}}{p} + ... + \frac{b_{m}}{p^{m}}} \right)_{10}\)
.
Exemple
Si on utilise une base supérieure à 10 on remplace A par 10 et B par 11 …
| Position | \(3\) | \(2\) | \(1\) | \(0\) | \(- 1\) | \(- 2\) | \(- 3\) |
| binaire | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
1101,101
| Exposant | \(2^{3}\) | \(2^{2}\) | 0 | \(2^{0}\) | \(\frac{1}{2^{1}} =2^{-1}\) | \(\frac{0}{2^{2}} = 0\) | \(\frac{1}{2^{3}} =2^{-3}\) |
| Base 10 | 8 | 4 | 0 | 1 | \(\frac{1}{2}\) | 0 | \(\frac{1}{8}\) |
\(\left( {8 + 4} \right),\left( {1 + \frac{1}{2} + \frac{1}{8}} \right) = 12 + \frac{8 + 4 + 1}{8} = 13,625\)
.
Exemple du calcul inverse :
traduire en binaire le nombre\(43,625\) qui est en base 10 :
Pout 43 on divise par 2 le reste est 1 et le quotient est 21 et on continue pour arriver à un quotient égal à 0.
43=2\(\times\) 21+1
21=2\(\times\) 10+1
10=2\(\times\) 5+0
5=2\(\times\) 2+1
2=2\(\times\) 1+0
1=2\(\times\) 0+1
\(0,625 \times 2 = 1,250 \geq 1\) , on obtient 0,1
\(0.250 \times 2 = 0,500 < 1\) ,on obtient 0,10
\(0,500 \times 2 = 1,000 \geq 1\) , on obtient 0,101
Le nombre décimal 43,625 est égal à 101011,101 en binaire.
.
Opérations
.
Addition
En binaire exemple d’addition
\(\left( 101 \right)_{2} + \left( 11 \right)_{2} = \left( 1000 \right)_{2}\,\,\) (en base 10) on obtient \(5 + 3 = 8\)

.
Soustraction
En binaire exemple de soustraction \(\left( 101 \right)_{2} - \left( 11 \right)_{2} = \left( 10\right)_{2}\,\,\) (en base 10) on obtient \(5 - 3 = 2\)
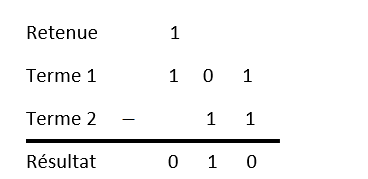
.
Multiplication
En binaire une multiplication est de cette forme \(1 0 1 \times 1 1= 1 1 1 1\) (en base 10) on obtient \(5 \times \ 3=15\)

.
Division
En base 2 voici la division \(\frac{110}{11}=10\) : (en base 10 on obtient \(\frac{6}{3}=2\) )

.
Représentation approximative
Précision et arrondi
En base 10 on a comme valeur approchée ou arrondie \(\frac{1}{3}=0,3333....\)
En binaire si on calcule un nombre rationnel on ne peut pas toujours trouver sa valeur exacte :
.
Par exemple :
\(\\\frac{1}{11}\approx 0, 0 1 0 1.\) et 0, 0 1 0 1 \(=0+\frac{1}{{{2}^{2}}}+\frac{1}{{{2}^{4}}}=\frac{1}{4}+\frac{1}{16}=\frac{5}{16}\approx0,3\)
Si on continue : \(0,0101010101=\frac{1}{{{2}^{2}}}+\frac{1}{{{2}^{4}}}+\frac{1}{{{2}^{6}}}+\frac{1}{{{2}^{8}}}+\frac{1}{{{2}^{10}}}=\frac{314}{1024}\approx0,333\)